Triangulation tab

Click Here for a "How-To" guide on creating Contour Grids

The Triangulation tab changes the grid from rectangular to a  triangular grid. Triangular grids always “honor the data” at the cost of sometimes unrealistic changes in slope or dip.  Refinement adds more interpolation inside these triangles, which smoothes these grids.  Interior angle clipping reduces grid artifacts caused by widely separated wells on the edge of the map.

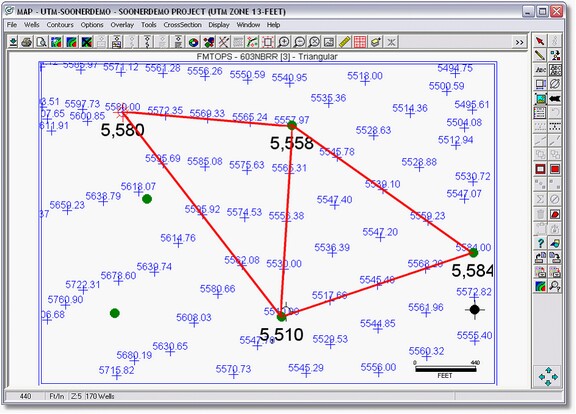
Instead of interpolating values for nodes at regularly spaced X and Y intervals, triangulation instead constructs a network of nearest neighbors using the data points.  Essentially, Petra calculates node values along lines (shown with lines) between data points.  These nodes form triangles known as “Delaunay triangles.”  Notice also that there is a node value directly on top of each well.  The resulting contours “honor the data” better because they are drawn using the actual values as opposed to interpolated data in rectangular gridding.  Triangular grids are better suited to closely spaced, or highly-variable data rather than widely separated data.

Check the Triangulate box to perform triangulation instead of rectangular gridding.

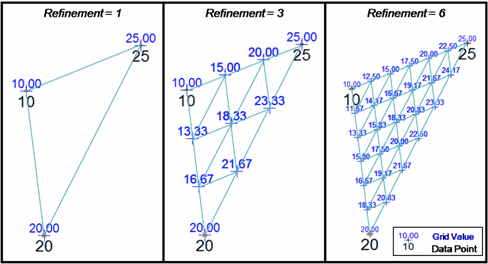
Triangle Refinement –   In a simple triangular grid, each Delaunay triangle is independent from every other triangle so calculated gradients on one triangle can differ significantly from an adjacent triangle.  This can lead to rapidly changing, geologically unrealistic dips and angular contour lines.  Contours from these simple triangular grids can look strange and can even cross.

Petra smoothes these triangular contours with a process called “triangle refinement.”  Refinement adds more points inside a Delaunay triangle to smooth the grid’s surface and contour lines.  These points inside the triangle are interpolated using Petra’s surface style (such as “Highly Connected Features”). selected on the Method tab and surrounding data points.  The refinement value selected here determines the number of additional points, which in turn governs the smoothness of the contours.  A refinement of 1 simply uses the existing data points with no interpolation, while a refinement of 16 adds a great deal of interpolated points inside each triangle.  Practically, a highly refined grid will have smoother contour lines than a grid with lower or no refinement.

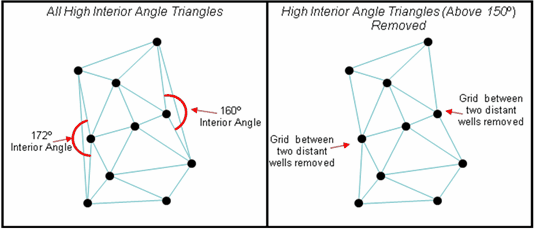
Interior Angle – Triangular grids attempt to connect all data points together regardless of how far apart they are. The part of the grid based on an interpolation between distant data points often shows geologically unrealistic contours – especially on the edge of the map.  On the right side of the example below, two highlighted triangles have high interior angles of 172 and 160 degrees.  The area of the grid represented by these two triangles probably interpolates the data too far and should be removed.

The triangular grid between these distant wells has one corner with a large angle.  Filtering out triangles with this high interior angle helps to trim out overly-interpolated or geologically unrealistic parts of the grid on the edge of the map.  Setting the value here to 150, as in the example below, will eliminate all triangles with an internal angle above 150 degrees.  The smaller the angle, more edge triangles are removed. Suggested values are 120 to 160 degrees.

Fast Local Slope Interpolation Method –Normal refinement uses the selected surface style to interpolate data points inside each Delaunay triangle based on the surrounding “neighborhood” of data points.  The “Fast Local Slope” method instead uses partial derivatives to interpolate inside each triangle.  In other words, while the normal refinement method attempts to make a more coherent regional picture based on outside data, this method simply uses only the data points in the Delaunay triangle.  Consequently, this method is quick, but is prone to geologically unreasonable dip changes and other artifacts.